Allacciare le scarpe ai fisici

Avete mai provato ad allacciare i lacci delle scarpe con una sola mano, bendati e magari sotto la pioggia? Ecco, più o meno così ci si sente a raccontare la storia della teoria delle stringhe. È come insegnare la fisica a Collino: sembra impossibile, ma se ci provi ti diverti lo stesso. Perché la teoria delle stringhe è un’avventura fatta di incidenti fortunati, intuizioni geniali, risate amare e colpi di scena degni di una serie TV.

Negli anni ’60, i fisici vivevano un’epoca di abbondanza… forse troppa. Ogni esperimento con gli acceleratori produceva nuove particelle, e i laboratori sembravano più collezionisti di francobolli che scienziati. Si parlava addirittura di “zoo delle particelle”: protoni, neutroni, pioni, kaoni, e chi più ne ha più ne metta.

In questo caos, un giovane teorico italiano, Gabriele Veneziano, pubblicò una formula che sembrava mettere ordine. Lui stesso raccontò che l’aveva pescata quasi per caso, studiando funzioni matematiche note, e non si aspettava di aver trovato un tesoro. Ma la sua equazione descriveva bene le interazioni forti, quelle che tengono insieme i quark.

Da lì nacque l’idea che le particelle non fossero puntini indivisibili, ma minuscole “cordicelle” vibranti. Come corde di violino, potevano suonare note diverse a seconda della vibrazione: un quark qui, un mesone là. Il sogno era che tutta quella giungla di particelle fosse solo un concerto di stringhe ben accordate.

Purtroppo, il sogno durò poco. Nel frattempo la cromodinamica quantistica (QCD) prendeva piede: i gluoni, con il loro collante colorato, spiegavano l’interazione forte molto meglio delle stringhe. Così, l’idea di Veneziano e colleghi finì in soffitta, considerata un esperimento elegante ma poco utile. Una parentesi che, all’epoca, sembrava chiusa.

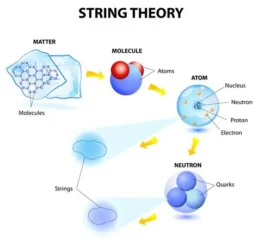
Mentre le stringhe uscivano di scena, restava l’obiettivo finale della fisica: conciliare la relatività generale di Einstein con la meccanica quantistica. Due teorie splendide, ma incompatibili. La relatività dice: “Lo spazio-tempo è un tessuto elastico che si piega con le masse.” La meccanica quantistica risponde: “Ok, ma a piccolissima scala tutto è agitato, casuale, pieno di fluttuazioni.”

Provate a unire le due cose: è come cercare di cucire seta con filo spinato. I calcoli vanno in tilt, saltano fuori infiniti che rendono impossibile fare previsioni. Per descrivere la gravità con gli strumenti quantistici serviva qualcosa di nuovo, un linguaggio diverso.

Fu allora che qualcuno rispolverò quell’idea strana delle stringhe. Se invece di punti infinitesimali, le particelle fossero cordicelle estese? Forse questo “spessore” avrebbe evitato gli infiniti mostruosi.

Negli anni ’80, John Schwarz e Michael Green ripresero sul serio la vecchia teoria. Lavoravano quasi nell’ombra, considerati eccentrici. Poi, nel 1984, pubblicarono un risultato che cambiò tutto: le stringhe potevano eliminare certe “anomalie” matematiche che mandavano in crisi altre teorie. Non solo: tra le vibrazioni possibili di una stringa compariva una particella con tutte le caratteristiche del gravitone, l’ipotetico messaggero quantistico della gravità.

Fu l’inizio della prima “rivoluzione delle stringhe”. Da teoria di nicchia, snobbata da quasi tutti, le stringhe diventarono la star della fisica teorica. Per anni furono viste come la candidata migliore per la famosa “teoria del tutto”, quella che avrebbe unificato in un’unica cornice tutte le forze della natura.

Poi arrivò Edward Witten, una sorta di guru della matematica e della fisica teorica. Con il suo talento visionario, riformulò e ampliò la teoria, introducendo la supersimmetria. In breve, il campo si trasformò in una giungla di idee: nuovi oggetti (come le brane), nuove dimensioni (non tre, non quattro, ma dieci o undici!) e una matematica tanto elegante quanto vertiginosa.

C’era però un problema. Invece di avere una sola teoria delle stringhe, ne erano spuntate ben cinque. Ognuna con caratteristiche diverse, simmetrie particolari, tecnicismi matematici
unici. Sembrava una sconfitta: cinque teorie in competizione invece di una sola teoria del tutto.

Ma nel 1995, durante una conferenza, Edward Witten sganciò la bomba: forse non erano cinque teorie diverse, ma cinque facce della stessa realtà. Con un colpo di genio introdusse la cosiddetta M-theory, una teoria ancora più profonda che le unificava tutte.

In questa nuova cornice, le stringhe non erano gli unici protagonisti: comparivano anche oggetti a più dimensioni, chiamati “brane” (da membrane). E lo spazio non era più a 10 dimensioni, ma addirittura a 11. Alcuni fisici iniziarono a scherzare sul significato della “M”: per qualcuno era “Magic”, per altri “Mystery”, o semplicemente “Mother of all theories”.

L’idea era potente: le cinque teorie delle superstringhe erano solo approssimazioni, viste da angolazioni diverse, di una teoria ancora più grande. Come guardare la stessa montagna da cinque vallate differenti: il profilo cambia, ma la vetta è sempre quella.

Ed eccoci alla questione cruciale. La teoria delle stringhe (o M-theory) è meravigliosa, elegante, seducente. Ma si può davvero chiamare scienza?

Da un lato, offre una cornice coerente per unificare la gravità con le altre forze. E nessun’altra teoria ci è riuscita con la stessa eleganza. Dall’altro, però, resta irrimediabilmente lontana dall’esperimento: le stringhe sarebbero minuscole, miliardi di volte più piccole di quanto possiamo indagare con gli acceleratori attuali. Non abbiamo prove dirette, e forse non le avremo per molto tempo.

Così la comunità scientifica si divide: alcuni la considerano l’unica via promettente, altri la bollano come matematica da salotto, più vicina alla filosofia che alla fisica.

E intanto la teoria resta lì, come un paio di scarpe futuristiche: splendide, scintillanti, ma ancora chiuse nella scatola. Nessuno le ha ancora indossate per correre davvero.

Alla fine, la storia della teoria delle stringhe è un’avventura che racconta più dei fisici che dell’universo stesso: la loro ostinazione, la loro creatività, la loro voglia di spingersi oltre.

Forse un giorno scopriremo che le stringhe erano la chiave di tutto. Forse no. Ma intanto, i fisici continuano ad allacciare i loro lacci, sperando che queste scarpe li portino fin dentro il cuore della realtà.