Sinusoidi ovunque: viaggio nella mente di Fourier

Cosa lega il principio di indeterminazione di Heisenberg, le AirPods e un capelluto matematico francese dell’Ottocento convinto che tutto, ma proprio tutto, potesse essere scomposto in sinusoidi?

Sembra l’inizio di una barzelletta, eppure è tutto vero: se hai mai ascoltato un podcast o della musica, ignorando il frastuono della metro è merito della matematica. In particolare, una matematica che, curiosamente, riappare anche quando proviamo a localizzare un elettrone. Infatti, quella stessa trasformata che scompone i rumori in frequenze è anche la chiave che ci spiega perché non possiamo mai sapere, nello stesso momento, dove si trovi una particella e quanto stia correndo.

Per capire come si arriva fin qui bisogna partire proprio da quel capelluto matematico francese: Fourier. Studiando il calore, il nostro scienziato si accorse di qualcosa di davvero potente: ogni onda può essere riscritta come combinazione lineare di seni e coseni. E cos’è una combinazione lineare?

Detto in modo semplice: una somma pesata. Tipo: se prendi 5 pere e ci sommi 3 mele, hai una combinazione lineare di frutta. Applichi lo stesso principio a delle onde (cioè funzioni) e voilà: puoi ricostruire qualsiasi forma complessa partendo solo da seni e coseni.

Per scomporre in sinusoidi le funzioni periodiche, Fourier inventò una serie:

La serie è una somma discreta, cioè una somma di tanti oggetti distinti, come se contassi uno per volta gli orsetti in un sacchetto Haribo. In questo caso però si tratta di una somma di seno e coseno. Andando ad analizzare la funzione precedente, i termini an e bn ci dicono quanto coseno e quanto seno è contenuto nell’onda che stiamo scomponendo. Più termini della serie aggiungiamo, più l’approssimazione sarà precisa, fino al caso limite di considerare infiniti termini, i quali ci permetterebbero di ottenere esattamente l’onda di partenza. Tutto questo funziona, però, solo se la funzione considerata è periodica.

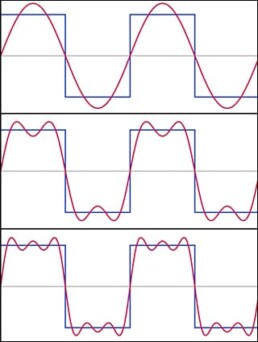
Ma se la funzione che voglio scomporre non lo fosse? In questo caso, entra in gioco la trasformata di Fourier, che è la versione con gli steroidi della serie.

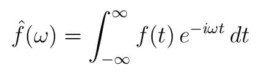
Quella specie di S che vedi dopo l’uguale è un integrale, ovvero una somma continua, il modo per calcolare il totale di una grandezza che varia continuamente. Per capirlo al volo ti basta pensare di dover pesare della sabbia: quale folle peserebbe un granello per volta? Invece, la metteresti semplicemente sulla bilancia, tutta insieme. Ecco, quella bilancia, in matematica, è proprio l’integrale.

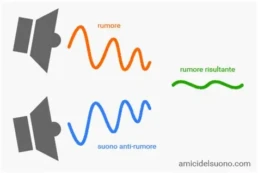
Bene, ora è arrivato il momento di parlare delle tue AirPods. In pratica, esse sono dotate di un microfono che registra i rumori esterni, ovvero che fa entrare un’onda sonora, un segnale fatto di vibrazioni dell’aria.

Una volta entrata, l’onda complessa del rumore viene scomposta nei suoi ingredienti di base, proprio come abbiamo imparato prima: in una somma di seni e coseni, ognuno con una certa frequenza e intensità. In poche parole, viene applicata la nostra eroina, la trasformata di Fourier.

Ma qual è lo scopo? Semplice, combattere il rumore con il rumore. Infatti, una volta conosciuto il nemico da vincere, le AirPods producono una versione negativa dell’onda di partenza, una copia perfetta ma sfasata. Le onde si scontrano tra di loro, e il risultato è un po’ di pace.

È il momento di confonderti le idee. Probabilmente hai già sentito parlare della meccanica quantistica, quella teoria che descrive la realtà su scala atomica e subatomica. Forse, però, non sai che ogni sistema quantistico, per esempio un elettrone, è descritto da una funzione d’onda, indicata con l’elegantissima lettera greca Ψ (psi).

Tutto super interessante, ma… non stavamo parlando della trasformata di Fourier? Esatto! È proprio lei la protagonista dietro una delle più interessanti stranezze quantistiche. Infatti, la funzione d’onda Ψ(x) ci dice “dove” potremmo trovare una particella, mentre la sua trasformata di Fourier, Ψ̃(p), ci racconta come si potrebbe muovere, cioè con quale quantità di moto.

E qui arriva la domanda che ha fatto tremare i pilastri della fisica classica: è possibile conoscere con precisione esatta sia dove si trova una particella sia con quanta quantità di moto si muove? Purtroppo (o per fortuna, perché questo rende tutto maledettamente interessante) la matematica risponde negativamente.

Il motivo lo dobbiamo proprio alla trasformata di Fourier. Infatti, più stringi la funzione d’onda nella posizione (cioè più sai esattamente dove si trova la particella), più si allarga la sua trasformata nella quantità di moto (cioè la tua conoscenza sul suo movimento diventa imprecisa). Se invece vuoi sapere con precisione come si muove (quanta quantità di moto ha), la posizione si fa sfocata.

Questo scambio inevitabile è proprio ciò che ci racconta il principio di indeterminazione di Heisenberg, formulato (indovina un po’) da Heisenberg nel 1927.

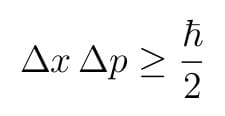
In parole semplici: il prodotto dell’incertezza sulla posizione (quanto è sparpagliata la tua conoscenza su dove si trova) e dell’incertezza sulla quantità di moto (quanto è incerta la tua conoscenza su come si muove) non può mai essere più piccolo di un certo valore costante. Tradotto: non puoi mai avere una precisione perfetta su entrambe le cose contemporaneamente.

Ti sembra strano? Lo capisco. Però è proprio così: la matematica non mente, e ci mostra che a volte la realtà è molto diversa da come la immaginiamo. E voglio essere chiaro: l’indeterminazione non è un limite dei nostri strumenti o della nostra capacità di misura, ma una proprietà profonda e intrinseca del mondo quantistico. Insomma, a livello microscopico, la natura non si comporta come una macchina precisa e prevedibile (cit. per Newton e Einstein) ma come un gioco di probabilità.

Siamo partiti dalle funzioni e siamo arrivati alla natura probabilistica della realtà, un viaggio affascinante, ma tutt’altro che astratto. La trasformata di Fourier, attraverso il suo elegante formalismo matematico, ci rivela infatti qualcosa di potente: ogni fenomeno, ogni suono, ogni segnale, persino una particella elementare può essere scomposto in componenti semplici, essenziali, in onde sinusoidali. E da queste onde, combinate con precisione, si può poi ricostruire l’intero.

Fourier ci offre uno strumento per leggere la realtà in profondità, per coglierne le strutture nascoste. Una realtà che, dietro la complessità apparente, rivela un or- dine sorprendente e un’intrinseca armonia.

I lettori interessati ad approfondire l’analisi complessa possono cliccare qui per saperne di più.

1. Bergamini, M., Trifone, A., & Barozzi, G. (n.d.). Matematica.blu 2.0 – Volume 4B. Zanichelli.
2. Bertsch, M., Dal Passo, R., & Giacomelli, L. (2ª ed.). (n.d.). Analisi matematica 1 e 2. McGraw-Hill.
3. Sakurai, J. J., & Napolitano, J. (n.d.). Meccanica quantistica moderna. Zanichelli.
4. Susskind, L., & Friedman, A. (n.d.). Meccanica quantistica. Raffaello Cortina Editore.